문제
마법사 상어는 파이어볼과 토네이도를 조합해 파이어스톰을 시전할 수 있다. 오늘은 파이어스톰을 크기가 2N × 2N인 격자로 나누어진 얼음판에서 연습하려고 한다. 위치 (r, c)는 격자의 r행 c열을 의미하고, A[r][c]는 (r, c)에 있는 얼음의 양을 의미한다. A[r][c]가 0인 경우 얼음이 없는 것이다.
파이어스톰을 시전하려면 시전할 때마다 단계 L을 결정해야 한다. 파이어스톰은 먼저 격자를 2L × 2L 크기의 부분 격자로 나눈다. 그 후, 모든 부분 격자를 시계 방향으로 90도 회전시킨다. 이후 얼음이 있는 칸 3개 또는 그 이상과 인접해있지 않은 칸은 얼음의 양이 1 줄어든다. (r, c)와 인접한 칸은 (r-1, c), (r+1, c), (r, c-1), (r, c+1)이다.
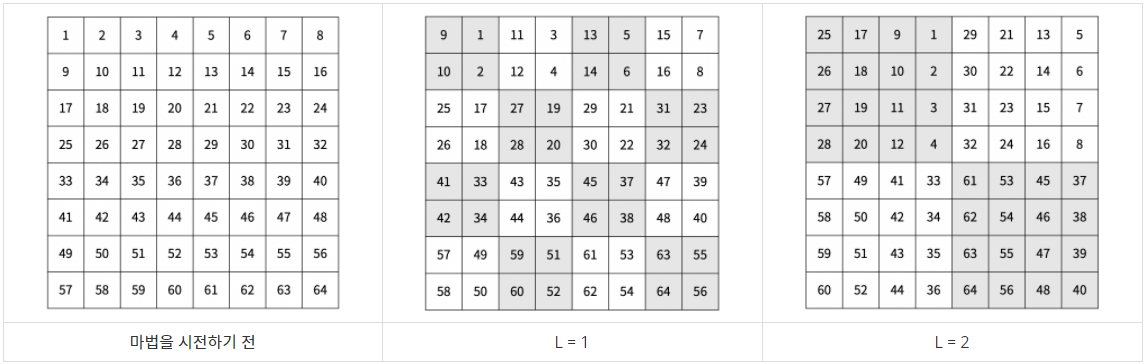
마법사 상어는 파이어스톰을 총 Q번 시전하려고 한다. 모든 파이어스톰을 시전한 후, 다음 2가지를 구해보자.
- 남아있는 얼음 A[r][c]의 합
- 남아있는 얼음 중 가장 큰 덩어리가 차지하는 칸의 개수
얼음이 있는 칸이 얼음이 있는 칸과 인접해 있으면, 두 칸을 연결되어 있다고 한다. 덩어리는 연결된 칸의 집합이다.
입력
첫째 줄에 N과 Q가 주어진다. 둘째 줄부터 2N개의 줄에는 격자의 각 칸에 있는 얼음의 양이 주어진다. r번째 줄에서 c번째 주어지는 정수는 A[r][c] 이다.
마지막 줄에는 마법사 상어가 시전한 단계 L1, L2, …, LQ가 순서대로 주어진다.
출력
첫째 줄에 남아있는 얼음 A[r][c]의 합을 출력하고, 둘째 줄에 가장 큰 덩어리가 차지하는 칸의 개수를 출력한다.
제한
- 2 ≤ N ≤ 6
- 1 ≤ Q ≤ 1,000
- 0 ≤ A[r][c] ≤ 100
- 0 ≤ Li ≤ N
풀이
삼성 코딩테스트에서 흔히 등장하는 2차원 배열 안에서의 시뮬레이션 문제이다. 이 문제는 크게 3가지 단계로 나눌 수 있는데 이는 다음과 같다.
- 격자의 정확한 회전
- 얼음의 적절한 융해
- 가장 큰 덩어리 찾기
이 3가지 중에서는 아무래도 격자의 회전이 제일 난이도 있는 구현 파트이다. 격자의 시계/반시계 방향 회전은 자주 출제되는 유형이기 때문에 처음 코드를 짜보고 난 뒤에는 아예 그 코드를 외워두는게 낫다. 구현은 간단하지만 매번 생각해내기에는 시간이 아깝고 충분히 실수가 발생할 수 있기 때문이다.
얼음의 융해는 어려울 점이 없지만 한가지 놓치기 쉬운 부분이 있는데, 바로 얼음이 동시에 융해한다는 것이다. 따라서 2중 for 문을 통해 순차적으로 바로바로 융해시켜주면 안되고, 어느 칸을 융해시킬 지 모든 칸에 대해 미리 정해놓은 다음 일괄적으로 융해시켜야 오류를 범하지 않는다. 미리 융해시켜버린 칸이 0 이 되었을 경우에는 인접한 칸에 영향을 미치기 때문이다.
가장 큰 덩어리 찾기는 일반적인 DFS/BFS 문제이다. 필자는 구현의 간결함을 위해 DFS 로 구현하였다.
전체 코드
1 | |
- Post link: https://blog.yjyoon.dev/boj/2020/11/04/boj-20058/
- Copyright Notice: All articles in this blog are licensed under CC BY-NC-SA 3.0 unless stating additionally.
