[삼성 기출] 백준 23288번 주사위 굴리기 2 풀이

| |
백준 온라인 저지 23288번 - 주사위 굴리기 2 C++ 풀이 (삼성 SW 역량테스트 기출)


문제

크기가 N×M인 지도가 존재한다. 지도의 오른쪽은 동쪽, 위쪽은 북쪽이다. 지도의 좌표는 (r, c)로 나타내며, r는 북쪽으로부터 떨어진 칸의 개수, c는 서쪽으로부터 떨어진 칸의 개수이다. 가장 왼쪽 위에 있는 칸의 좌표는 (1, 1)이고, 가장 오른쪽 아래에 있는 칸의 좌표는 (N, M)이다. 이 지도의 위에 주사위가 하나 놓여져 있으며, 주사위의 각 면에는 1보다 크거나 같고, 6보다 작거나 같은 정수가 하나씩 있다. 주사위 한 면의 크기와 지도 한 칸의 크기는 같고, 주사위의 전개도는 아래와 같다.

1
2
3
4
  2
4 1 3
  5
  6

주사위는 지도 위에 윗 면이 1이고, 동쪽을 바라보는 방향이 3인 상태로 놓여져 있으며, 놓여져 있는 곳의 좌표는 (1, 1) 이다. 지도의 각 칸에도 정수가 하나씩 있다. 가장 처음에 주사위의 이동 방향은 동쪽이다. 주사위의 이동 한 번은 다음과 같은 방식으로 이루어진다.

  1. 주사위가 이동 방향으로 한 칸 굴러간다. 만약, 이동 방향에 칸이 없다면, 이동 방향을 반대로 한 다음 한 칸 굴러간다.
  2. 주사위가 도착한 칸 (x, y)에 대한 점수를 획득한다.
  3. 주사위의 아랫면에 있는 정수 A와 주사위가 있는 칸 (x, y)에 있는 정수 B를 비교해 이동 방향을 결정한다.
    • A > B인 경우 이동 방향을 90도 시계 방향으로 회전시킨다.
    • A < B인 경우 이동 방향을 90도 반시계 방향으로 회전시킨다.
    • A = B인 경우 이동 방향에 변화는 없다.

칸 (x, y)에 대한 점수는 다음과 같이 구할 수 있다. (x, y)에 있는 정수를 B라고 했을때, (x, y)에서 동서남북 방향으로 연속해서 이동할 수 있는 칸의 수 C를 모두 구한다. 이때 이동할 수 있는 칸에는 모두 정수 B가 있어야 한다. 여기서 점수는 B와 C를 곱한 값이다.

보드의 크기와 각 칸에 있는 정수, 주사위의 이동 횟수 K가 주어졌을때, 각 이동에서 획득하는 점수의 합을 구해보자.

이 문제의 예제 1부터 7은 같은 지도에서 이동하는 횟수만 증가시키는 방식으로 구성되어 있다. 예제 8은 같은 지도에서 이동하는 횟수를 매우 크게 만들었다.


입력

첫째 줄에 지도의 세로 크기 N, 가로 크기 M (2 ≤ N, M ≤ 20), 그리고 이동하는 횟수 K (1 ≤ K ≤ 1,000)가 주어진다.

둘째 줄부터 N개의 줄에 지도에 쓰여 있는 수가 북쪽부터 남쪽으로, 각 줄은 서쪽부터 동쪽 순서대로 주어진다. 지도의 각 칸에 쓰여 있는 수는 10 미만의 자연수이다.


출력

첫째 줄에 각 이동에서 획득하는 점수의 합을 출력한다.


풀이

시뮬레이션과 약간의 그래프 탐색이 결합된 문제이다. 지도에서의 점수 계산은 응용 없이 순수한 DFS 코드만으로 구할 수 있어서 간단하다. 이 문제의 핵심은 바로 주사위 시뮬레이션에 있다.

필자는 초기에 주사위 아랫면의 숫자에 따라 동서남북 이동 후의 아랫면 숫자가 일정하다고 생각했다. 하지만 이는 잘못된 발상이었고 주사위가 마지막으로 이동한 방향에 따라서 이는 얼마든지 달라질 수 있었다. 따라서 이러한 접근을 버리고 주사위의 전개도를 저장하고, 이동 시에 이를 통째로 갱신하는 방식으로 접근했다. 되게 번거롭게 들릴 수 있지만 어차피 주사위는 6면밖에 되지 않고, 가장 직관적인 방법이기 때문에 실수할 확률을 줄일 수 있다.

구현을 위해서는 주사위 이동 방향에 따른 격자의 변화 패턴만 파악하면 됐었고, 이는 다음과 같다.

1

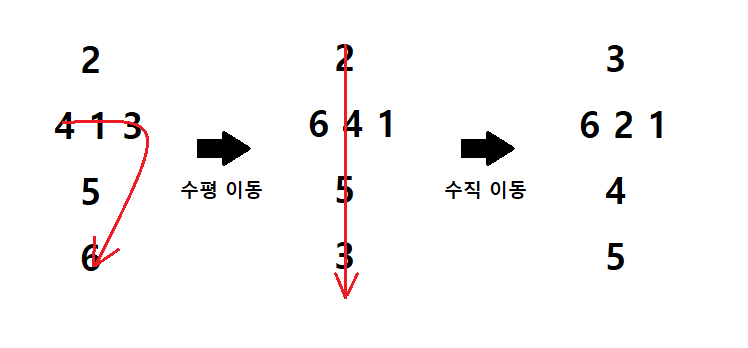
각각은 동쪽 이동과 남쪽 이동이고, 서쪽과 북쪽의 경우 화살표의 방향만 반대로 변한다. 보다시피 그리 복잡한 패턴이 아니라 쉽게 구현할 수 있었다.

이런 구현 방식을 택할 경우 주사위의 아랫면은 전개도 배열의 (3,1) 위치로 고정된다.


전체 코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
#include <iostream>
#include <cstring>
using namespace std;

int N,M,K;

int dy[] = {0,1,0,-1};
int dx[] = {1,0,-1,0};

// 주사위 전개도
int dice[4][3] = {
    {0,2,0},
    {4,1,3},
    {0,5,0},
    {0,6,0}
};

int board[20][20];
bool visited[20][20];

// 방향 범위 초과 예외 처리
void dirSetting(int& dir) {
    if(dir==4) dir=0;
    else if(dir==-1) dir=3;
}

bool inRange(int y, int x) {
    return 0<=y && y<N && 0<=x && x<M;
}

// 점수 계산 DFS
int dfs(int y, int x) {
    int ret = 1;
    visited[y][x] = true;

    for(int i=0;i<4;i++) {
        int ny = y+dy[i];
        int nx = x+dx[i];
        if(!inRange(ny,nx) || visited[ny][nx] || board[ny][nx]!=board[y][x])
            continue;
        ret += dfs(ny,nx); // 칸 수 누적
    }

    return ret;
}

// 주사위 아랫면은 (3,1)로 고정
int getBottom() {
    return dice[3][1];
}

// 이동 방향에 따른 전개도 변화
void move(int dir) {
    int temp = getBottom();
    switch(dir) {
    case 0:
        dice[3][1] = dice[1][2];
        dice[1][2] = dice[1][1];
        dice[1][1] = dice[1][0];
        dice[1][0] = temp;
        break;
    case 1:
        dice[3][1] = dice[2][1];
        dice[2][1] = dice[1][1];
        dice[1][1] = dice[0][1];
        dice[0][1] = temp;
        break;
    case 2:
        dice[3][1] = dice[1][0];
        dice[1][0] = dice[1][1];
        dice[1][1] = dice[1][2];
        dice[1][2] = temp;
        break;
    case 3:
        dice[3][1] = dice[0][1];
        dice[0][1] = dice[1][1];
        dice[1][1] = dice[2][1];
        dice[2][1] = temp;
        break;
    }
}

int main() {
    ios_base::sync_with_stdio(0);
    cin.tie(0); cout.tie(0);
    
    cin>>N>>M>>K;
    for(int i=0;i<N;i++)
        for(int j=0;j<M;j++)
            cin>>board[i][j];

    int score = 0;

    int dir = 0;
    int num = getBottom();
    int y = 0, x = 0;
    while(K--) {
        // 이동할 수 없을 시 반대 방향으로 전환
        if(!inRange(y+dy[dir],x+dx[dir])) {
            for(int i=0;i<2;i++) {
                dir++;
                dirSetting(dir);
            }
        }

        y+=dy[dir]; x+=dx[dir];
        move(dir);
        num = getBottom();

        memset(visited,0,sizeof(visited));
        score += dfs(y,x)*board[y][x];

        if(num > board[y][x]) dir++;
        else if(num < board[y][x]) dir--;
        
        dirSetting(dir);
    }

    cout<<score;

    return 0;
}
0%